Das Modell hat immer recht

geschrieben am 01.09.2021

Bevor die STIKO eine Impfempfehlung ausspricht, führt sie eine Nutzen-Risiko-Abwägung durch. Das war wohl auch der Plan, als es zum zweiten Mal um eine Covid-19-Impfempfehlung für Jugendliche ging. Nun sah man sich aber dem Dilemma ausgesetzt, dass auf Grundlage der verfügbaren Daten zwar das Risiko als sehr gering eingeschätzt wurde, aber auch der Nutzen. Da man nicht so genau weiß, was herauskommt, wenn man Null durch Null teilt, man andererseits aber "der Politik entgegenkommen" wollte, gab man der Versuchung nach, den Daten die Ergebnisse einer Modellierung beizumischen.

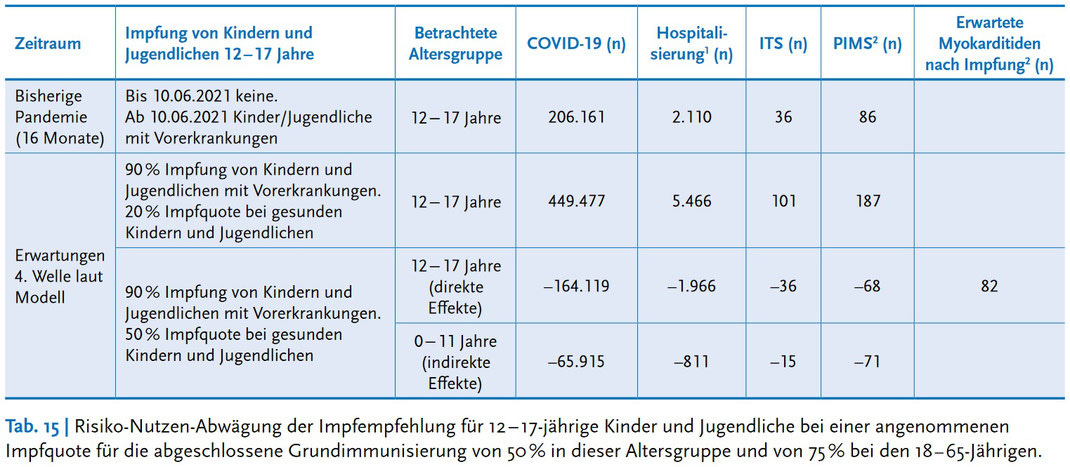
Was sind aber die Eigenschaften von Modellen (englisch "Models"), wie es William Briggs gerne ausdrückt? Sie sind beeindruckend anzusehen, sie sind komplett künstlich, und sie tun immer nur genau das, was man ihnen sagt. An der folgenden Tabelle (aus der Begründung der Impfempfehlung, Tabelle 15 auf Seite 41) wollen wir versuchen zu verstehen, was man dem Modell gesagt hat, auf das die STIKO baut.

Im Modell wird eine 4. Welle prognostiziert, und zwar mit einer Inzidenz von teilweise über 400. Das lässt sich sicher nicht ausschließen, stellt aber nur ein mögliches Szenario dar. In finanzmathematischen (Risiko-) Modellen würde man ähnlich vorgehen, nämlich ein Risikomaß (zum Beispiel Erwartungswert, Quantil oder Expected Shortfall) wählen. Leider werden wir nicht informiert, welche Statistik hier zum Einsatz kam. Ich möchte das gewählte Szenario auch gar nicht weiter kritisieren, sondern die weiteren dargestellten Zahlen unter der Annahme untersuchen, dass es tatsächlich eintritt.

Zunächst einmal waren die 2.110 Hospitalisierungen nur eine mögliche Wahl für die Vergangenheit (also die Daten, mit denen man das Modell kalibriert). Es handelt sich um die IfSG-Meldezahl (siehe Abschnitt 3.1 des Bulletins). Eine Alternative hätte die Zahl der DGPI dargestellt (siehe Abschnitt 3.2 des Bulletins). Aber vielleicht waren 440 Hospitalisierungen ein bisschen zu mager? In den 2.110 sind jedenfalls auch (was in der Fußnote anerkannt wird) zufällig festgestellte Infektionen enthalten. Bei einer Hospitalisierungsquote von - vorsichtig angenommen - 10 Prozent auf ein Jahr, etwa 5 Millionen Jugendlichen im Alter von 12 bis 17 Jahren und einer durchschnittlichen Inzidenz (inklusive moderater Dunkelziffer) von 100 wären etwa 600 solche Fälle in fünfzehn Monaten zu erwarten.

Selbst wenn die 2.110 Hospitalisierungen eine vernünftige Annahme darstellen sollten, wurde dem Modell offenbar beigebracht, für die Zukunft noch eine Schippe draufzulegen. Der Quotient aus Hospitalisierungszahl und Fallzahl steigt nämlich von 102 bp (Basispunkte, d.h. 0,01%) auf 122 bp, die ITS-Quote von 1,75 bp auf 2,25 bp. Was könnte dahinter stecken? Etwa doch die Annahme, dass die Delta-Variante zu einem höheren Anteil an Hospitalisierungen führt, auch wenn die STIKO selbst (auf Seite 22) schreibt, dass es für eine solche Annahme keine Hinweise gibt? Bei den PIMS-Fällen bleibt die Quote interessanterweise gleich.

Hinzu kommt noch, dass in der "bisherigen Pandemie" praktisch keine Impfungen angerechnet werden konnten, in der 4. Welle aber (zumindest ab einem gewissen Zeitpunkt) mit einer Impfquote von 90% bei Jugendlichen mit Vorerkrankung und 20% bzw. 50% bei gesunden Jugendlichen gerechnet wird. Die Daten der DGPI legen nahe, dass der größte Teil der ITS-Fälle der "bisherigen Pandemie" Vorerkrankungen hatte. Wirkt denn nun die Impfung nicht, oder sind die im Modell angenommenen zukünftigen Auswirkungen des Virus auf gesunde Jugendliche noch sehr viel drastischer?

Aber die Impfung wird ja wohl doch als hochwirksam angenommen. Wenn ich gnadenlos eine (sofort erreichte) Impfquote von 100% bei gesunden Jugendlichen annehme und dazu den Effekt von -164.119 für eine Erhöhung der Impfquote um 30 Prozentpunkte mit 8/3 multipliziere, dann ergibt das eine Reduktion um 437.650. Da bleibt ja von den 449.477 kaum noch etwas übrig! Hurra, Corona lässt sich besiegen, wenn nur ganz viel und ganz schnell geimpft wird! In Tabelle 14 auf Seite 29 des Bulletins wird übrigens ein deutlich schwächerer Effekt bei einer Erhöhung der Impfquote auf 80% angenommen, aber woran liegt das? Nur daran, dass die Impfungen nicht sofort erfolgen können?

Bleiben noch die erwarteten Myokarditiden nach Impfung, die offenbar als einzige darstellenswerte Nebenwirkung angesehen werden. Warum ist das entsprechende Feld in der zweiten Zeile leer? Wird der Wert als irrelevant angesehen? Sind die 82 ein Inkrement zu dem nicht vorhandenen Wert aus der zweiten Zeile, so wie in den anderen Spalten, oder sind sie eine Gesamtzahl?

Mit Modellen wie diesem, die sehr viele Parameter haben und mit einer unguten Mischung aus zahlreichen Annahmen (beispielsweise zu Wirksamkeit von Impfungen, Unterschieden zwischen Virusvarianten) und gleichzeitig Vereinfachungen (beispielsweise, wie ich vermute: keine getrennte Simulation der Jugendlichen mit und ohne Vorerkrankung) arbeiten, lässt sich jedes gewünschte Ergebnis produzieren. Eine Hilfe zur Nutzen-Risiko-Abwägung ist das sicher nicht.